עיתונאיות ועיתונאים, הירשמו כאן להודעות לעיתונות שלנו
הירשמו לניוזלטר החודשי שלנו:

בעיית הריצוף מרתקת מתמטיקאים ואמנים מהזמן הקדום ועד לימינו. לכאורה, מדובר בשאלה פשוטה יחסית: האם אפשר לרצף מישור אין-סופי תוך שימוש בחוקים מוסכמים? בעת העתיקה, עוד לפני הספירה הנוצרית, התגלו המצולעים המשוכללים שמרצפים את המישור לבדם: משולשים, מרובעים ומשושים. אפשר היה לחשוב שאין עוד מה לחדש בתחום זה, אלא שהמתמטיקה תמיד מפתיעה אותנו, כך שמדי פעם מתגלה עוד ריצוף מסוג חדש, בדרך כלל כתוצאה משינוי החוקים.
במחצית השנייה של המאה הקודמת התגלו שתי דרכים חדשות לבצע ריצוף. האחת: ריצוף שבו התבניות אינן חוזרות על עצמן במדויק, המכונה "ריצוף לא מחזורי". דוגמה ידועה בתחום זה היא הריצוף שהציע רוג'ר פנרוז. ריצוף זה תרם לגילוי של גבישים קוואזי-מחזוריים על-ידי פרופ' דן שכטמן מהטכניון, שזכה על כך בפרס נובל בכימיה לשנת 2011. הדרך השנייה קרויה "ריצוף של דמיון עצמי". דרך זו הוצעה על-ידי ויליאם תורסטון. באחרונה הציע פרופ' אנתוני ג'וזף, מהמחלקה למתמטיקה במכון ויצמן למדע, ריצוף חדש: "ריצוף אמיתי עם משולשים בעלי דמיון עצמי". פרופ' ג'וזף נתן לריצוף הזה את השם "ריצוף בר שגיא" – על-שם נכדתו שהלכה לעולמה בגיל 15 לאחר מחלה.
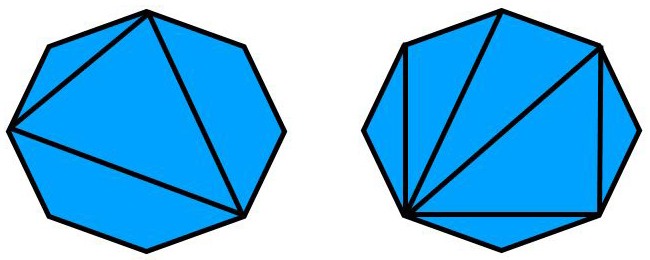
"ריצוף בר שגיא" הוא שם כללי לריצוף שמבוסס על קבוצת משולשים הנגזרים ממצולע משוכלל (שווה צלעות ושווה זוויות). כדי ליצור את קבוצת המשולשים, יש לשרטט משולש חסום בתוך מצולע משוכלל בעל מספר (n) צלעות, בדרך של מתיחת קווים בין שלושה קדקודים עוקבים במצולע (אבל לאו דווקא צמודים). משרטטים את כל המשולשים החסומים האפשריים בצורה כזו. אם r,s,t הם מספר צלעות המצולע שבין שלושה קדקודים עוקבים, אזי תמיד r+s+t=n.
כדאי לשים לב לכך, ששני משולשים בקבוצה יחפפו אם ורק אם השלשות r,s,t שלהם שוות עד כדי תמורה (כלומר, שאפשר להחליפן זו בזו). אין צורך כמובן לספור משולשים חופפים. כמו כן, כאשר r,s,t שונים, המשולש הוא בהכרח משולש שונה צלעות, ואז נוח להבחין בין משולש כזה ובין תמונת הראי שלו. באיור אפשר לראות דוגמה של המשולשים הנגזרים ממתומן משוכלל: ארבעה משולשים במתומן הימני ועוד משולש אחד במתומן השמאלי. שניים מהמשולשים הם שוני צלעות, ולכן צריך להוסיף את תמונות הראי שלהם, ולפיכך יש בסך הכל שבעה משולשים בקבוצה. עבור מעושר (n=10), נגזרים שמונה משולשים שונים, ארבעה מהם שוני צלעות, כלומר, בסך הכל 12 משולשים.
עכשיו מסדרים את אורכי הצלעות של כל המשולשים הנגזרים, בקבוצה משל עצמה לפי קנה מידה שנבחר כך שאורך הצלע הקטן ביותר הוא יחידה אחת. ניקח אחד המשולשים מהקבוצה הנגזרת מהמצולע, לא משנה איזה, ונגדיל אותו בקנה מידה של אחד האורכים מתוך קבוצת אורכי הצלעות, לא משנה איזה. מתקבל משולש דומה למשולש המקורי.
פרופ' ג'וזף הוכיח שאפשר לרצף את המשולש המוגדל (וכן צורות המורכבות מחיבור המשולשים), עם המשולשים שבקבוצה המקורית, מבלי שיהיו רווחים כלשהם בין המשולשים המרצפים ומבלי שקודקוד של משולש יפגוש צלע של משולש אחר (דרישה זו מכונה ריצוף ״אמיתי״ – proper). פרופ' ג'וזף מציע שיטה (אלגוריתם) שמאפשרת ליצור ריצופים כאלה בהינתן מצולע משוכלל מקורי (ממחומש ומעלה).
בנוסף, הוכיח פרופ' ג'וזף (בתוספת כמה תנאים טבעיים נוספים) שהריצוף באמצעות המשולשים הנגזרים מהמצולע הוא הריצוף היחיד האפשרי. כמו כן, הוא הוכיח שהריצוף אפשרי כשהיחס שבו מגדילים את המשולש יכול להיות כל אורך צלע של כל אחד מהמשולשים שנגזרו מהמצולע.
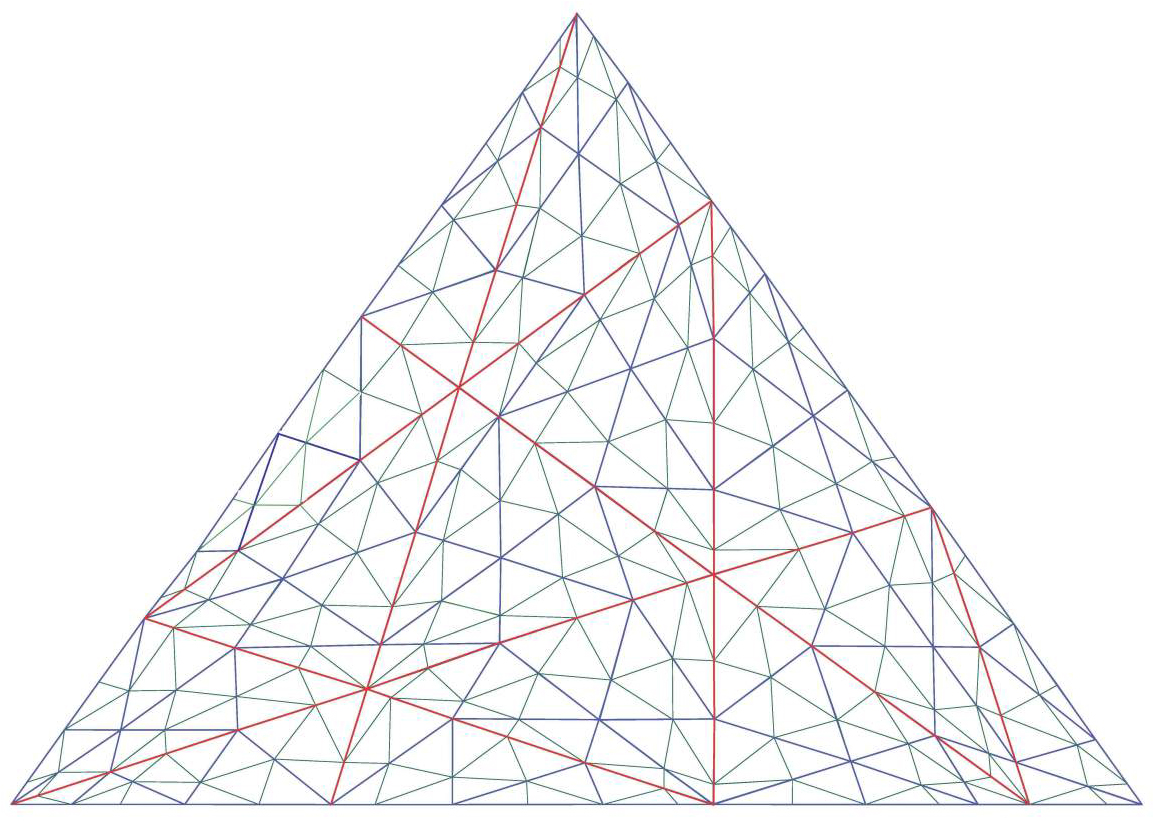
אם חושבים על זה, אפשר להבין שאת התהליך הזה אפשר לעשות שוב, לכל אחד מהמשולשים המרצפים את המשולש המוגדל, כלומר, אפשר לרצף כל אחד מהמשולשים המרצפים בעותקים "מוקטנים" מקבוצת המשולשים (מוקטנים לפי יחס של אורכי אחת מצלעות אחד המשולשים). למעשה, אפשר לבצע את התהליך שוב ושוב (בכמה חזרות, או "איטרציות") וכך לקבל "ריצופי בר שגיא" מורכבים, מפליאים ביופיים. כדי לאפשר מספר אין-סופי של חזרות, תוך שימוש בכל אורך צלע שנרצה (עבור יחס ההגדלה) ובכל סדר אפשרי, אי-אפשר פשוט לעשות שוב ושוב את אותו הדבר. יש צורך באילוצים נוספים – ומדובר בעבודה מורכבת. תגליות והוכחות אלה הן הרחבה של עבודתו של תורסטון.באיור אפשר לראות דוגמה לריצוף כזה שנוצר ממתומן משוכלל ומרוצף באמצעות הקבוצה של המשולשים הנגזרים ובשלוש חזרות.

פרופ' ג'וזף המשיך להוכיח שאפשר לצבוע "ריצופי בר שגיא" לאחר חזרה אחת, תוך שימוש בשני צבעים בלבד – ואולם, בכל חזרה נוספת יש צורך בשלושה צבעים לפחות. טרם הוכח אם די בשלושה צבעים לכל ריצוף, או שיש מצבים שבהם יש צורך בארבעה צבעים. במובן המתמטי, הכוונה ב"צביעה" היא ״צביעת מפות״, כלומר, צביעה כך ששטחים סמוכים לא יהיו באותו צבע, ובמקרה זה, צביעה כך שלשני משולשים הצבועים באותו צבע לא תהיה צלע משותפת (משפט ארבעת הצבעים שוולפגנג האקן וקנת אפל הוכיחו ב-1976 ואשר לפיו, אין צורך ביותר מארבעה צבעים לצביעת מפה).
פרופ' ג'וזף הוקסם לא רק מהיופי ומהמתמטיקה של "ריצוף בר שגיא", אלא גם מהאפשרות להפוך אותו למשחק הרכבה. הוא חתך את משולשי הבסיס של ריצוף כזה מנייר צבעוני, הדביק אותם למגנטים וכך אִתגר את נכדתו, שהייתה אז בת שש, להרכיב מחדש את הריצוף על המקרר בבית. בין השאר, רצה פרופ' ג'וזף לבדוק את היתכנות השימוש בריצוף זה כעזר להמחשת "דיאגרמות משקל במישור", שבהן משתמשים ב"אלגברות לי" (Lie Algebra), תחום המחקר העיקרי שלו. ניסיונו לא צלח, ואולם, שיטות ההרכבה המתמטיות שבהן השתמש הובילו לגילוי בלתי-צפוי של מתודה להרכבת חתכי ויירשטראס (שדוגמה מפושטת שלהם היא חצי קו אורך מהקוטב הצפוני לקוטב הדרומי, החותך כל קו רוחב בנקודה אחת בלבד ובכך מגדיר אותו).
עבודתו זו של פרופ' ג'וזף ליצירת גרסאות לא-קומוטטיביות של אלגברה גיאומטרית, הובילה להבנה שבתנאים מסוימים עשוי להתקיים דמיון בין המכניקה הקלאסית ובין מכניקת הקוואנטים – על אף שבתנאים רגילים יש ביניהן הבדלים משמעותיים ומוחשיים.

ההשראה ל"ריצופי בר שגיא" באה גם מהשירים היפים שכתבה נכדתו של פרופ' ג'וזף, בר, שמבטאים, בחלקם, את הסבל הנפשי והגופני שחוותה כאשר חלתה בסרטן הדם, ואשר נמצאו לאחר מותה. שיריה נאספו ופורסמו ומהווים "חומר קריאה הכרחי לכל רופא שמתעתד לטפל בחולי סרטן", כדברי האונקולוג קרלוס קלדס מאוניברסיטת קיימברידג׳, בריטניה
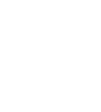
"משפט ארבעת הצבעים" הנודע קובע כי לעולם לא נזדקק ליותר מ-4 צבעים כדי לצבוע "ריצוף בר שגיא".