קללת הממדיות, ברכת הממוצעים

כאשר מתמטיקאים מדברים על המימד של מרחב, הם מתכוונים למספר הקואורדינטות הנחוצות על מנת לתאר נקודה או דגימה ממרחב זה. היקום (במובן הקלאסי) הוא תלת-ממדי. מרחב המצבים של מערכת בעלת 100 חלקיקים, כשהמצב של כל חלקיק מתואר באמצעות מיקום ומהירות, הוא מימד 100*2*3=600. מרחב התמונות האפשריות בעלות 1,000*1,000 פיקסלים הוא מימד שלושה מיליון (בהנחה שכל פיקסל מתואר באמצעות שלושה צבעי יסוד); והמימד של רצפי הדי-אן-אי האפשריים של אדם נמדד במאות מיליונים.

בעידן המידע וה"ביג דאטה", ניתוח של מידע במרחבים בעלי מימד גבוה צובר תאוצה וחשיבות. במרחב תלת-ממדי קל לנו לדמיין, למשל, איך נראית קבוצת הנקודות שנמצאת במרחק קבוע מנקודה מסוימת (קבוצה זו נקראת סְפֵירה). אבל האם יש דרך לדמיין איך נראית קבוצת הנקודות במרחב התמונות שבהן מופיע כלב? מה לגבי קבוצת התוצאות של ספירת דם (נניח שבספירת דם יש כ-100 מדדים שונים) אשר מְשַקפות סיכון מוגבר לחלות בסוכרת? האם יש דרך להבין "איך נראית" קבוצה זו ולאפיין את הגיאומטריה שלה?

האתגר העיקרי בניתוח מידע במימד גבוה הוא ריבוי של מספר האפשרויות. ניקח למשל את מרחב התמונות, ונניח לרגע שכל פיקסל יכול לקבל רק שני ערכים – שחור או לבן. מספר האפשרויות לתמונה במקרה זה יהיה 2 בחזקת מספר הפיקסלים. גם בתמונה ברזולוציה גרועה יחסית נגיע בדרך זו למספרים אסטרונומיים. באופן כללי, אפשר לומר שכדי "לסרוק" את כל הנקודות האפשריות במרחב, מספר הדגימות שנצטרך יהיה אקספוננציאלי במימד. תופעה זו נקראת "קללת הממדיוּת", The curse of dimensionality.

השאלה הגדולה היא, האם אפשר למצוא עקרונות שיעזרו לנו להתגבר על קללת הממדיות. לפי תיאוריה מתמטית חדשה יחסית, במקרים רבים, במערכות בעלות מימד גבוה ניתן למצוא תופעות אשר מעידות על קיום מבנה בעל סדר ופשטות בתוך ריבוי האפשרויות העצום הזה. מתברר שכאשר מסתכלים על המערכת מנקודת המבט הנכונה, באופן מפתיע צץ סדר מתוך אי-הסֵדֶר. זה בדיוק מה שעושה ד"ר רונן אלדן מהמחלקה למתמטיקה במכון ויצמן למדע. על מחקריו בתחום זה (חקר מערכות במימד גבוה), הוא זכה באחרונה בפרס ארדש, הפרס החשוב ביותר שמעניק האיגוד הישראלי למתמטיקה.

תופעות במימד גבוה באות לידי ביטוי בסטטיסטיקה, במדעי המחשב ובפיסיקה, וההבנה שלהן חשובה גם בתחומים כמו למידת מכונה. אנחנו מחפשים במערכות האלה מוטיבים מתמטיים שחוזרים על עצמם ועשויים לייצג תכונות עומק"

אחד העקרונות העומד מאחורי תופעות אלה הוא עקרון המיצוע, או "חוק המספרים הגדולים": ככל שמספר המשתנים במערכת גדֵל, הממוצע שלהם יהיה פחות אקראי. למשל, אם נמצע את אחוז השינוי היומי בבורסה במשך תקופה ארוכה, נקבל ביטוי כמעט קבוע (או בעל שונותּ נמוכה מאוד). תופעה פשוטה זו עומדת בבסיס תיאוריה שנקראת "ריכוז מידה" (אחד מחלוציה הוא פרופ' ויטלי מילמן מאוניברסיטת תל-אביב), והיא מסייעת למתמטיקאים להתגבר על קללת הממדים הגבוהים.

עד כמה, ואיך, אפשר לנצל תופעות אלה לשם פתרון בעיות סטטיסטיות או אלגוריתמיות? למשל, בניתוח תמונה, במקום למדוד כל פיקסל בנפרד, מתברר שלפעמים דרך טובה יותר להתמודד עם המידע היא לבחור אזורים בתמונה באופן אקראי, ולמצע אותם בדרך מסוימת. "תופעות במימד גבוה באות לידי ביטוי בסטטיסטיקה, במדעי המחשב ובפיסיקה, וההבנה שלהן חשובה גם בתחומים כמו למידת מכונה", אומר ד"ר אלדן. "אנחנו מחפשים במערכות האלה מוטיבים מתמטיים שחוזרים על עצמם. מוטיבים כאלה עשויים לייצג תכונות עמוקות, המשותפות למערכות במימד גבוה". במחקריו גילה ד"ר אלדן קשרים לא-צפויים בין התנהגותן של מערכות במימד גבוה לבין תנועה בראונית. תנועה זו (המכונה לעיתים גם "הליכת שיכור"), היא דיפוזיה של חלקיקים זעירים השקועים בנוזל. המודל המתמטי שמתאר את התנועה הזאת ("תהליך וינר") משמש לתיאור תופעות רבות בפיסיקה, בביולוגיה ובכלכלה.

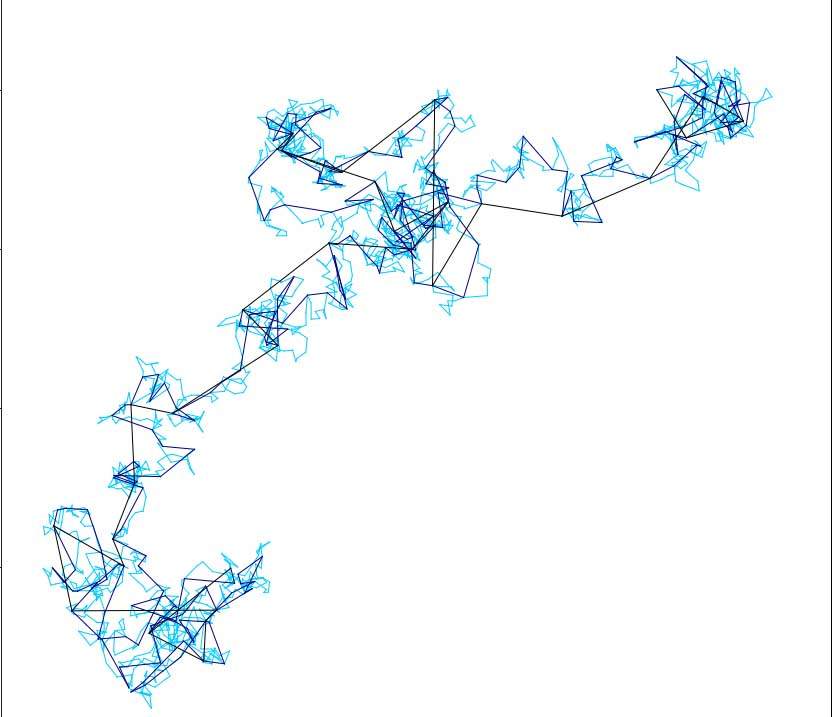
ד"ר אלדן מפתח שיטה שמאפשרת לנתח תופעות המתחוללות במערכות במימד גבוה באמצעות תנועה בראונית. בזכות מה שידוע על הקשר בין תנועה בראונית ודיפוזיה לבין תופעה שמתחוללת במערכת במימד גבוה עשויות לעלות תובנות ביחס לתכונות של אותה מערכת. בקבוצת מחקרים אחרת מתמקד ד"ר אלדן בניסיון להבין כיצד התיאוריה של ממדים גבוהים יכולה לסייע בפיתוח אלגוריתמים של אופטימיזציה ולמידה. במובן זה אפשר אולי לומר, שד"ר אלדן הגיע להישגים משמעותיים בדרך להפיכת "קללת הממדיוּת" לברכה.