01-01-1999
חוקרי המתמטיקה של מכון ויצמן למדע מפתחים תחומי מחקר קלאסיים ומודרניים של המתמטיקה ומדעי המחשב, תוך יצירה מתמדת של ידע חדש. מחקרים אלה, שבמידה רבה הם בסיסיים ותיאורטיים, מצמיחים לעתים פירות שחלקם לא צפויים וחלקם מיושמים ומסייעים באופן דרמטי להתקדמותם של שטחי מדע אחרים. לדוגמה, כבר בשנת 1954 בנו המתמטיקאים של מכון ויצמן מדע את "ויצק", המחשב האלקטרוני הראשון בישראל, שהיה אחד המחשבים הראשונים בעולם כולו. "ויצק", שנועד ליישומים מדעיים הוא הגזע שממנו הסתעפו, לימים, תעשיות החומרה והתוכנה של ישראל. פיתוחים אחרים המבוססים על תרומותיהם של חוקרי מדעי המחשב הפועלים בימים אלה במכון: "כרטיסים חכמים" המגבילים גישה לנתוני מחשב ולשידורי טלוויזיה של לוויינים מסחריים; שיטות חדשות לדחיסת מידע; ארכיטקטורת תוכנה מתקדמת המבוססת על "שפה חזותית" מקורית שעשויה לסייע בתכנון מערכות בסדרי גודל שונים, כמו מטוסים, טילים, שבבי מחשב, רשתות תקשורת ורשתות של מסילות ברזל; וטכנולוגיה שמאפשרת למשתמשי רשת האינטרנט "להיפגש" חזותית ולנהל שיחות ועסקות ב"אתרי מפגש דמיוני". מדעני הפקולטה למדעי המתמטיקה במכון מפעילים שיטות מתמטיות חדשניות לחקר התנועות של הזרוע האנושית. מחקרים אלה מסייעים בתכנון גפיים מלאכותיות, מקדמים את ההבנה של מחלות בקרה מוטורית ומסייעים בתכנון בקרה ותנועה של רובוטים. מתמטיקאים אחרים משתפים פעולה עם חוקרי מוח בפיתוח שיטות של ראייה רובוטית ממוחשבת, בטכניקות של בינה מלאכותית. תחום מחקר מתמטי נוסף שבו עוסקים חוקרי המכון קשור לבקרת מערכות מתוחכמות המותקנות במטוסים, במעבורות חלל ובכורי כוח גרעיניים, וכן גם להבנת ולחיזוי פעולתן של מערכות ביולוגיות מורכבות.
מדעי המתמטיקה
חיפושי נפט
בשנותיה הראשונות של המדינה ביצעו המתמטיקאים של המכון סקרים גיאופיסיים וסייסמולוגיים במטרה לאתר מרבצי נפט. כתוצאה מהמחקרים האלה התגלה בשנת 1955 שדה הנפט הראשון בישראל, בחלץ. מחקרים אלה שימשו בסיס שעליו הוקם בהמשך המכון למחקרי נפט וגיאופיסיקה, שהוא תאגיד מחקר ממשלתי.
מאזינים לקול האדמה
סייסמולוג מהמכון הקים והפעיל את המצפה הגיאופיסי בקרבת אילת, לצורך מעקב והבחנה בין פעילות סייסמית טבעית לבין תנודות קרקע הנובעות ממעשה ידי אדם. במצפה נאספו ונותחו נתונים על הפעילות הסייסמית של שברים גיאולוגיים באזורנו, על פעילות מגנטית ואקוסטית באטמוספירה, וגם על פיצוצים גרעיניים. על בסיס הנתונים שנאספו, נותחו ומופו הסיכונים הסייסמים בארץ. בעקבות זאת פותחה תיאוריה סייסמית, שלפיה מוקד הרעש של כל רעידת אדמה נע בעת הרעש לאורך השבר הגיאולוגי במהירות גדולה. תיאוריה זו אומתה בהמשך.
הנתונים שנאספו במצפה הגיאופיסי על הפיצוצים הגרעיניים הניסיוניים שביצעו ברית-המועצות וסין, הושוו עם נתוני הפיצוץ המסתורי שהתחולל בטונגוסקה, סיביר, בשנת 1908. על בסיס ההשוואה חושבו אנרגיית הפיצוץ והגובה שבו התחולל מעל לקרקע.
פתרון המשוואות של הטבע
החוקים היסודיים של הפיסיקה, הכימיה וההנדסה, אמנם מוגדרים בבירור, אבל יישומם לפתרון בעיות שונות, מעשיות ותיאורטיות, מחייב חישובים מורכבים ומסובכים כל כך, עד שלמעשה אי-אפשר לבצעם בדייקנות מלאה.
מדעני המכון פיתחו גישות חדשניות לארגון הייררכי של המרחב-זמן, המאפשרות לצמצם במידה ניכרת את המורכבות של החישובים האלה. גישות אלה משמשות עתה מדענים רבים בפישוט חישובים בפיסיקה של חלקיקים אלמנטריים, דימות רפואי, אנליזת מכ"ם, אסטרופיסיקה, חיזוי מזג-אוויר וחיפושי נפט. גישות חדשות אלה גם עשויות לאפשר לחוקרים להבהיר את הארכיטקקטורה ואת תגובות-הגומלין של מבנים כימיים, דבר שעשוי לסייע בתכנון חומרים תעשייתיים ותרופות חדשות.
שאלה של מחיר
בניגוד לתפיסה המקובלת, יש סחורות שהביקוש להן מתגבר דווקא כשמחירן עולה. הפרדוקס הזה, המוכר זה מאה שנים בקירוב, מכונה "אפקט גיפן" (על שמו של הכלכלן האנגלי סר רוברט גיפן שחי בסוף המאה ה- 19). מתמטיקאים מהמכון הצליחו לפתח מודל מתמטי שמגדיר את התנאים הממשיים להופעתה האפשרית של התופעה הנדירה הזאת, לאחר שגילו אותה בכלכלה היפנית המודרנית. בהתבססם על ניתוח סטטיסטי של ההוצאה למשק-בית במדינה זו, גילו המדענים כי הביקוש למשקה האלכוהולי הזול שוצ'ו, החביב במיוחד על היפאנים דלי ההכנסות, עלה כתוצאה מעליית מחירו. זאת, מכיוון שעניי יפן חדלו לקנות משקאות יקרים יותר, והשקיעו את כל תקציב המשקאות שלהם בשוצ'ו.
המתמטיקאים פיתחו מודל מתמטי שמאפשר להם לקבוע את מידת ייתכנותו של אפקט גיפן במשק נתון. המודל אינו מביא בחשבון את השפעת ה"יוקרתיות" של מוצרים מסוימים על הצריכה, וגם לא את הנטייה של חלק מהצרכנים להעדיף סחורות יקרות, בהנחה שאיכותן עולה על איכותן של סחורות זולות יותר.
חילחול
חילחול (פרקולציה) הוא תהליך הזרימה של נוזל דרך חרירים בחומר מוצק לא הומוגני. המודלים המתמטיים של חילחול, דומים למודלים של מגנטיות ושל חילוף מצבי צבירה. לכן, העמקת הבנה באשר לאחד מהתהליכים האלה תורמת להרחבת הבנתם של האחרים.
מדעני המכון פיתחו שני מודלים מתמטיים חדשים של חילחול, שלהם יתרונות רבים בהשוואה למודלים הקודמים. חקר המודלים המקוריים של מדעני המכון הביא לגילוי חוק חדש המקשר בין הגיאומטריה של החומר המוצק (שדרכו הנוזל מחלחל), לבין התחום שאליו יגיע הנוזל המחלחל.
הצגות
ה"חבורה" היא מושג בסיסי במתמטיקה. היא מגדירה פעולות מתמטיות כגון חיבור או כפל בין מספרים באופן אבסטרקטי, ולכן אפשר להשתמש בה בניתוח מערכות מתמטיות מורכבות. חבורות מופיעות בתדירות בכל שטחי המתמטיקה העיונית והשימושית ובמדעי המחשב, וכן בענפי מדע אחרים, כגון כימיה ופיסיקה. המבנה המתמטי של חבורות (ושל מערכות דומות אחרות) נחקר במסגרת תורת ההצגות. בתורה זו ממומשות החבורות באמצעות מטריצות, שהן טבלאות של מספרים שעליהן מוגדרות פעולות מתאימות. הצגות הן מכשיר רב-עוצמה במתמטיקה ובשימושים רבים של המתמטיקה. למשל, תורת ההצגות מהווה את הכלי הבסיסי לתיאור חלקיקים אלמנטריים בפיסיקה, ובאמצעותה ניבאו את קיומם של חלקיקים רבים שלאחר מכן התגלו בניסויים. מתמטיקאים במכון עוסקים בפיתוח תורת ההצגות וביישומי התורה לשטחים שונים, כגון תורת המספרים, תורת החבורות, תורת החוגים וקומבינטוריקה.
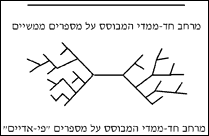
מרחב מסתעף
אנו רגילים להתבונן ולנתח גיאומטריה המתוארת בקואורדינטות של מספרים ממשיים, כשההפרשים בין המספרים האלה קובעים את המרחק הגיאומטרי בין נקודות שונות במרחב. אבל, מדעני המתמטיקה מכירים גם מספרים שמבנה המרחקים ביניהם שונה. מספרים אלה קרויים מספרים "פי-אדיים", והמרחקים ביניהם מבוססים על קשר מתמטי ביניהם לבין מספרים ראשוניים. האם אפשר לפתח גיאומטריה המתוארת בקואורדינטות של מספרים "פי-אדיים"? מדעני המכון הראו כיצד אפשר לעשות זאת. ממחקר מקורי זה עולה, למשל, שבעוד מרחב חד-ממדי המבוסס על מספרים ממשיים הוא קו פשוט, הרי שמרחב חד-ממדי המבוסס על מספרים "פי-אדיים", מתאפיין במבנה המסתעף והולך ללא גבול.
גיאומטריה רב-ממדית
כאשר מסובבים גוף במישור מספר פעמים סביב נקודה הנמצאת בו, ומסמנים את השטח המשותף לשרשרת הגופים שהתקבלה, מבחינים מיד כי מתקבלת צורה הדומה לעיגול שמרכזו בנקודת הסיבוב. קל לדמיין כי התופעה נכונה גם בשלושה ממדים, כאשר הגוף המשותף לכל הסיבובים הוא כדור. מתברר, כי תופעה דומה מתקיימת גם במרחבים בעלי ממדים רבים יותר.
כמה סיבובים צריך להפעיל כדי לקבל קירוב טוב של הכדור המשותף? מתמטיקאים במכון חוקרים את הבעיה המתמטית המורכבת הזאת, וכן בעיות דומות אחרות בתחום הגיאומטריה של גופים קמורים בממדים גבוהים. במחקרים אלה מצאו מדעני המכון, כי מספר הסיבובים הדרושים תלוי אך מעט בגוף שבו מתחילים את התהליך. שיטת המחקר בתחום זה מבוססת על שיקולים הסתברותיים, ואם כי אי-אפשר להצביע על דרך מסוימת שבה יתקבל הקירוב הדרוש, אפשר להראות כי הקירוב מתקבל בהסתברות גדולה - אם הסיבובים נבחרים באקראי.
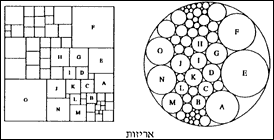
אריזה
כאשר מניחים מעגלים בעלי גדלים שונים במישור, כך שלא יחתכו זה את זה, יהיו ביניהם זוגות מעגלים שישיקו זה לזה וכאלה שלא יהיו ביניהם נקודות מגע. אפיון יחסי ההשקה האפשריים באריזה שכזו מהווה בעיה קומבינטורית מעניינת, המתקשרת לתחומים אחרים של המתמטיקה ושימושיה. המתמטיקאים של המכון תרמו רבות לפיתוח תחום המחקר הזה, והראו כיצד לנתח את המקרה שבו הגופים הנארזים אינם בהכרח מעגליים. להכללה זו נמצאו השלכות מפתיעות בתחום תורת הפונקציות המתמטיות ושימושיהן בפיסיקה.
תכנון ובקרה
המתמטיקה משמשת לתיאור תהליכים בטבע, וכן גם כעזר לתכנון ולשליטה כאשר האדם מבקש לרתום את כוחות הטבע לשירותו. למשל, תכנון של כלי תעופה, תחנות כוח, השקיה ועוד, נעשה תוך שימוש בעקרונות מתמטיים. למעשה, רוב הבדיקה של איכות התכנון נעשית באמצעות הדמיה ממוחשבת. מדעני המכון תרמו תרומות חשובות בתחום המתמטיקה של התכנון והבקרה.
רעיונות מתמטיים שפיתחו מדעני המכון בשנות השבעים והשמונים מיושמים כיום בתכנון מעשי ובבדיקה של יציבות מטוסים, יציבות של מערכות מתקדמות אחרות דוגמת מכשירים אופטיים המותקנים על כלי רכב, יציבות ותיקון אוטומטי של מתקני השקיה, ועוד.
מחקרים אחרים של מדעני המכון התמקדו בתכנון אופטימלי של תנועה רובוטית; למשל, תכנון של מעבר רובוט רחב מידה בשטח זרוע מכשולים, ופיתוח יכולת תגובה להפרעות הנקרות בדרכו של הרובוט.
מדעני המכון בחנו את יציבותם של תהליכים רציפים, כגון מעבר חום או תנועה גלית. מכיוון שתהליכים אלה מאפשרים רצף של הפרעות ותגובות, נדרשו המדענים לברר ולהגדיר מהן צורות היציבות האפשריות.
מחקר נוסף בתחום זה התמקד בתכנון ובבקרה של יחסי הגומלין בין גופים הנעים באטיות יחסית לבין תהליכים המתחוללים במהירות רבה. למשל, תכנון חקלאי לעומת שינויים תכופים במזג האוויר, או תנועת מכונית לעומת קצב סיבובי המנוע שלה. לצורך ניתוח תופעות כאלה פיתחו מדעני המכון מודל מתמטי המביא בחשבון את הבדלי סקאלות הזמן השונות שבהן מתחוללים התהליכים.
תחום חדשני שבו עוסקים מדעני המכון באחרונה, הוא חקר מערכות שבהן תהליכים רציפים שזורים בתהליכים בדידים. לדוגמה, תכנון, פיקוח ובקרה של זרימה רציפה באמצעות מחשב הפועל באופן דיגיטלי.
מדעני המכון עוסקים בתחומים אלה ברמה המתמטית האבסטרקטית. המחקר משלב תחומים רבים של המתמטיקה העיונית ואף תורם להם. באותה מידה, הרעיונות המועלים במחקר המתמטי מוצאים את דרכם לספרי ההנדסה ולשולחנות המהנדסים האמונים על היישום בתחומים השונים.
קבלת החלטות
תוספת מידע משפרת את יעילות הפעולה של מקבלי החלטות בתחומים רבים. מצד שני, מידע הוא "מוצר" יקר, שרכישתו בכמויות גדולות מדי עלולה להפוך תהליך רווחי לתהליך מפסיד. במכון פותח מודל מתמטי המגדיר את המידע כמשתנה החלטה, המאפשר לנתח את יחסי הגומלין הכמותיים בין מידע לבין התועלת שאפשר להפיק ממנו, במצבים שבהם יש צורך לקבל החלטות אופטימליות במצב של אי- ודאות.
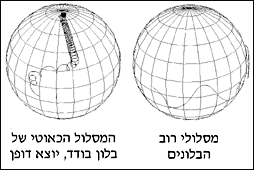
מסלולים
תנועה של גופים בטבע מתבצעת במסלולים שהתוואי שלהם ניתן למחקר מתמטי באשר הוא פתרון של משוואות הנקראות משוואות דיפרנציאליות. מדעני המכון חוקרים מסלולים אלה מכמה נקודות מבט.
אחד המחקרים בתחום זה מתמקד בבעיה מפורסמת המהווה זה זמן רב אתגר למתמטיקאים מכל העולם. הבעיה נוסחה בידי המתמטיקאי דוד הילברט, שהיה מהמתמטיקאים המובילים בעולם, בזמנו. מדובר בבעיה הידועה כבעיה השש עשרה ברשימת הבעיות שניסח הילברט בתחילת המאה. הבעיה עוסקת במציאת המספר האפשרי של מסלולי תנועה מחזוריים במישור, כאשר המשוואה הדיפרנציאלית מוגדרת באמצעות ביטויים שהם פולינומים. הפתרון המלא לבעיה זו עדיין רחוק, אך המתמטיקאים של המכון קידמו במידה רבה את הידע הנחוץ כדי לפותרה. בפרט, התקבל פתרון כמעט מלא למקרה שבו המשוואה מתארת הפרעה קטנה למשוואה המשמרת אנרגיה.
במחקר אחר הציעה מתמטיקאית מהמכון הסבר לניסוי שבוצע בשנות השבעים, ושבו שולחו בלונים לאטמוספירה באזור קו המשווה. רוב הבלונים נעו, כצפוי, באזור קו המשווה, אך אחדים מהם התקדמו בקו ישר לכיוון הקטבים, ובמהירות שאי-אפשר היה להסבירה על פי נתוני הרוחות שנשבו במסלולי התקדמותם. ההסבר שהציעה המדענית מהמכון תולה את סיבת הסטייה במסלוליהם של הבלונים שנעו אל הקוטב, בתהודה של תנועה כאוטית, הנובעת מצירוף של תנועת כדור-הארץ עם העובדה שפני כדור-הארץ אינם מעוצבים ככדור מדויק.
ערכים עצמיים
עצמים רוטטים, למשל מיתר שנמתח ומתכווץ, הם היוצרים את הצלילים שאנו שומעים. גובה הצליל תלוי בתדירות הרטיטה. זה זמן רב ידוע שהקצבים שבהם גוף יכול לרטוט הם קבועים ותלויים בהרכבו ובצורתו של החומר הרוטט. תופעות דומות של קצבים קבועים מראש מופיעות גם בתחומי טבע אחרים. למשל, גובה רמות האנרגיה של האלקטרונים באטום, או אורכי גל הקובעים את צבע האור הנפלט מחומרים שונים. לכל התופעות האלה יש מכנה מתמטי משותף: התדירויות נקבעות על פי תכונות של תבניות מסוימות, למשל מטריצות, ועל פי הדרך שבה התבניות האלה מותחות או מכווצות את המרחב שעליו הן פועלות. תכונות מתיחה אלה נקבעות על- ידי מקדמים מספריים הנקראים "ערכים עצמיים".
מדעני המכון הציעו דרך לגלות את תכונותיהם של ערכים עצמיים גבוהים, הקשורים לצלילים גבוהים, או לרמות אנרגיה גבוהות. דרך זו גם מקשרת את התכונות הגיאומטריות ואת התכונות המכניות של החומר, להופעת התדירויות הגבוהות. למחקר זה נודעת חשיבות להבנת תופעות בתחומים שונים, כגון מכניקה, אלקטרוניקה, אופטיקה, אקוסטיקה ועוד.
ראייה ורובוטיקה
ראייה ממוחשבת 1
מתמטיקאים במכון תיכננו דרכים ושיטות, שמאפשרות למערכות של ראייה ממוחשבת ("עיניים ממוחשבות") לזהות עצמים על בסיס שימוש בכמות מוגבלת של תצלומים מזוויות שונות. שיטות אלה עשויות לאפשר לרובוטים לנוע ולמצוא את דרכם במסלולים משתנים של אולמות ייצור, וכן לזהות עצמים באמצעות מערכות ממוחשבות. המדענים שעוסקים בתחום זה משתפים פעולה עם חוקרי מוח במכון, ומשיתוף הפעולה הזה עולה האפשרות שהמוח האנושי פועל - בתחום זיהוי העצמים - בדרכים דומות לאלה שפיתחו המתמטיקאים.
ראייה ממוחשבת 2
עד כה היה ידוע שהמוח שקולט נתונים חזותים חדשים, ממקם אותם בתחילה ב"אזור ראייה ראשוני", ורק לאחר מכן מעביר אותן ל"אזור ראייה עליון". אבל התברר שקיימים גם מסלולי העברה הפוכים: מ"אזור הראייה העליון" אל "אזור הראייה הראשוני".
מתמטיקאים מהמכון מציעים הסבר לתופעה זו, באמצעות מודל פעולה שלפיו נתונים חזותיים חדשים מוזרמים מ"אזור הראייה התחתון" אל "אזור הראייה העליון", בעוד שנתונים חזותיים שמאוחסנים בזיכרון מוזרמים בכיוון הפוך: מ"אזור הראייה העליון" ל"אזור הראייה התחתון". בדרך זו, שני הזרמים חולפים זה על פני זה במהירות רבה מאוד, מה שמאפשר למוח להשוות תמונות רבות ולזהות במהירות דמיון או התאמה ביניהן.
למודל המוצע הזה נודעת חשיבות רבה הן בחקר המוח והן בפיתוח יישומי רובוטים שונים, שאמורים להתבסס על חיקוי יכולתו ודרך פעולתו של המוח האנושי.
תנועה חלקה
מתמטיקאים מהמכון פיתחו מודלים מתמטיים המתארים את הדרך שבה המוח האנושי מתכנן את תנועת הגפיים ומפקח עליה. מודלים אלה מושתתים על הדרך שבה המוח יוצר - בתוכו - דגם של המרחב, ולאחר מכן מתכנן ומניע באמצעות העצבים, השרירים והשלד, את הגפיים במרחב. המודלים מבוססים גם על תיאוריה מקורית שפיתחו החוקרים, הקובעת שהגורם העיקרי שלפיו המוח מתכנן את מסלולי התנועה של הגפיים העליונות בתנועות מסוימות, כגון תנועת הושטת הזרוע, הוא "חלקות התנועה" מושג המתייחס לקצב שינוי תאוצת היד כפי שהוא מבוטא בקואורדינטות מרחביות.
באמצעות ניתוח מדויק של התנועה אפשר לחזות במידת קירבה רבה את מסלולי ומאפייני התנועה שייבחרו ויבוצעו בידי אנשים. בניסויים אחרים משמש ניתוח מדויק של התנועה לבחינת ההבדלים בין הדרך שבה אנשים בריאים מניעים את גפיהם, לבין הדרך שבה עושים זאת אנשים הסובלים ממחלות מוח ניווניות, דוגמת מחלת פרקינסון. בחינת ההבדלים האלה מסייעת בהבנת הקשר שבין פגיעה באזור מסוים של המוח, לבין התחוללות כשל באחד מהמרכיבים של תכנון וביצוע התנועה.
המתמטיקאים העוסקים במחקרים אלה משתפים פעולה עם חוקרים מתחומי מחקר אחרים, לרבות מדעי החיים וחקר המוח, במטרה לגלות ולהבין את ה"שפה המוטורית", או את הצופן הארגוני שבאמצעותו המוח מתכנן ומארגן את תנועת הגוף.
ההבנות המושגות במחקרים אלה משמשות את החוקרים גם במחקרים שתכליתם פיתוח רובוטים, שיוכלו לתכנן ולבצע תנועות ביעילות.
מדעי המחשב
חלוצי המחשב
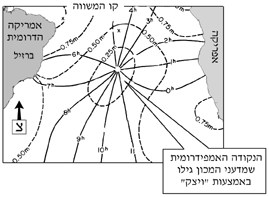
"ויצק", אחד המחשבים האלקטרוניים הראשונים בעולם, והראשון בישראל, תוכנן ונבנה במכון בשנת 1954 ופעל עד שנות השישים המוקדמות. "ויצק" שימש למחקר מתמטי, כגון פתרון בעיות הקשורות בגאות ובשפל. כדי לפתור את הבעיות האלה יש לבצע חישובים רבים ומסובכים מאוד, שאין טעם לנסות ולבצעם ללא מחשב. החישובים שבוצעו בידי מדעני המכון, באמצעות "ויצק", ושנמשכו אלפי שעות מחשב, איפשרו להם לשרטט מפות המתארות בקירוב רב את תנודות הגאות והשפל בעולם. בדרך זו גילו מדעני המכון את מיקומה המדויק של נקודה אמפידרומית (נקודה שלעולם לא מתחוללים בה גאות ושפל), בדרום האוקיינוס האטלנטי. מדידות שבוצעו בעקבות התגלית, אימתו את קיומה ואת מיקומה של הנקודה הזאת.
במחקר אחר השתמשו מדעני המכון ב"ויצק" לחישוב הספקטרום של אטום הליום, הכולל שלושה גופים: גרעין ושני אלקטרונים הנעים סביבו. פתרון מערכת היחסים הדינמית בין שלושה גופים, נחשב למשימה מתמטית מורכבת מאוד, ולמעשה, עד היום - עם כל ההתקדמות בתחום המחשבים - עדיין אין בידינו פתרון מלא לבעיות מסוג זה.
במחקרים נוספים בוצעו באמצעות "ויצק" חישובים שנועדו לבחינת מודלים תיאורטיים שונים באשר למבנה הפנימי של כדור הארץ, על שכבותיו השונות. מחקרים אלה התבססו על חישוב התפשטות של גלי הלם דרך השכבות הגיאולוגיות השונות, ועל השוואת התוצאות לתוצאות של מדידות אמת שבוצעו בעקבות רעשי אדמה שהתחוללו במקומות שונים בעולם. בתחום אחד החזיק "ויצק" בשיא עולמי: הוא היה מסוגל לטפל במלים ארוכות יותר, בהשוואה לאורך המלים המרבי שמחשבים אחרים בני זמנו היו מסוגלים לקלוט.
שני ממשיכי דרכו של "ויצק" - "גולם א" ו"גולם ב" - שגם הם תוכננו ונבנו במכון, היו גם הם החדישים והמתקדמים ביותר מסוגם, בעת השלמתם בשנת 1964 ("גולם א") ובשנת 1972 ("גולם ב"). מחשבים אלה שימשו את צורכי המחקר במכון ובמרכזי מחקר ישראליים אחרים.
אימות מערכות
מתמטיקאים מהמכון פיתחו שיטות מתוחכמות ל"אימות מערכות ממוחשבות" הכוללות חומרה ותוכנה כאחת. כידוע, ככל שהמערכות הממוחשבות מתפתחות, הן נעשות מורכבות ומסובכות יותר; וככל שהן מפקחות על תהליכים הרי-גורל יותר (לדוגמה, בקרה של כור גרעיני, שילוח טילים לחלל, ניהול מסלול טיסה של מטוס, בקרת ייצור במפעל תעשייתי, פיקוח על מיכשור רפואי בבתי חולים, פיקוח על מערכות תקשורת וכו'), כך גדל הסיכון שתקלה במערכות האלה תגרום נזקים כבדים ולעתים גם אובדן חיי אדם.
כדי למנוע את התרחשותן של תקלות מסוג זה, אפשר לנסות לבדוק את המערכות בשורה ארוכה של הדמיות (סימולציות). אלא ששיטה זו משאירה פתח לטעויות ולתקלות שעלולות להיות קטלניות. מדעני המכון פיתחו דרכים "לאמת" את נכונות המערכת באופן לוגי, כפי שמוכיחים משפט מתמטי.
בעבודות אלה השתמשו מדעני המכון בשפה מתמטית הקרויה "לוגיקת זמן", שבה אפשר לנסח ולהוכיח משפטים שטוענים טענות הקשורות גם בממד הזמן. שיטות אימות אלה משמשות כבר לאימות מערכות ממוחשבות בפרויקטים בינלאומיים רבי היקף.
הצפנה ופיענוח
מדען מהמכון, יחד עם עמיתים ממוסדות מחקר אחרים בעולם, פיתח שיטה מקורית להצפנת מידע ולפיענוחו על בסיס הכפלה של שני מספרים ראשוניים גדולים מאוד, זה בזה (מספר ראשוני מתחלק רק באחד ובעצמו). בטיחות ההצפנה בשיטה זו נובעת ממשך הזמן הרב שיידרש לאדם לא מורשה לפיענוח הצופן (משך זמן זה מוערך באלפי שנים).
שיטה זו מיושמת כיום, בין היתר, ב"כרטיסים חכמים" המותקנים במכשירי טלוויזיה ביתיים והמאפשרים רק ללקוחות מורשים לקלוט ולפענח את שידוריו של לוויין תקשורת מסחרי. ה"כרטיס החכם" מאפשר לחברה המפעילה את הלוויין לחייב כל לקוח, אך ורק בעד התוכניות והסרטים שבהם צפה. שיטת ההצפנה והפיענוח הזאת מיושמת גם בתחומי הכלכלה, הבנקאות והתקשורת המדינית.
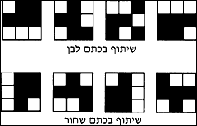
הצפנה חזותית
מדעני המכון פיתחו שיטה מקורית להצפנה ולפיענוח של מידע חזותי, שכדי ליישמה אין צורך במחשבים או באמצעים טכנולוגיים מתקדמים אחרים. השיטה מבוססת על פירוק המידע החזותי לכמה חלקים, בדרך שמאפשרת לקבוע כמה חלקים יידרשו כדי להרכיב מחדש את המידע המקורי. למשל, אפשר לחלק תמונה לחמישה חלקים, ולקבוע שכדי להבין את המידע האצור בתמונה, יש צורך בשילוב של שלושה חלקים לפחות. מספר החלקים המינימלי הדרוש לפיענוח נקבע על פי דרישות הסודיות והנוחיות של בעלי המידע.
שיטה זו משמשת כיום, בין היתר, להצפנה ולפיענוח של מידע חזותי המועבר בפקסמיליה.
אבטחת תקשורת
מדענית מהמכון פיתחה שיטה מקורית להוכחת טענות מתמטיות, הקרויה "הוכחות אינטראקטיוויות באפס ידיעה". השיטה מאפשרת, למשל, לוודא זהות מבלי שהמזדהה יסגיר מידע על עצמו. בדרך זו יכולים, למשל, משתמשים במאגרי מידע להזדהות בכניסה למאגר, להיכנס אליו ולבצע בו פעולות שונות, מבלי שיתקיים מעקב ותיעוד של פעולותיהם. יכולת זו חשובה מאוד לגורמים כלכליים, משפטיים, מדיניים ועוד.
הזיהוי בשיטה זו מתבצע בתהליך של מעין "שיחה" המתנהלת בין המזדהה לבודק. הבודק מפנה אל המזדהה שאלות אקראיות, דבר שמסכל כל אפשרות לשחזר את "שאלון הזיהוי". אם הנבדק מצליח לענות נכונה על כל שאלותיו של הבודק, הרי שזהותו הוכחה. בשיטת ה"הוכחות אינטראקטיביות באפס ידיעה", כאשר הטענה לזהות מסוימת היא נכונה, תמיד אפשר יהיה לשכנע בנכונותה; ולעומת זאת, כאשר הטענה לזהות אינה נכונה (כלומר, כשמישהו מנסה להתחזות), קיימת אפשרות גבוהה מאוד שהמתחזה ייכשל בתשובה לאחת משאלותיו של הבודק.
שיטת ה"הוכחות אינטראקטיוויות באפס ידיעה" מיושמת גם באבטחה של מידע במערכות של מחשבים מבוזרים. בדרך זו אפשר להניח לגורמים שונים לתרום מידע למאגר כללי כלשהו, אך בה בעת להגביל את יכולת משיכת המידע שלהם מאותו מאגר. לדוגמה, חישוב מדויק ואמין של ספירת קולות בבחירות, מבלי שאפשר יהיה לזהות מצביעים ואת אופן הצבעתם; החלטה על זוכה במכרז כלכלי כלשהו, מבלי לחשוף את פרטי הצעותיהם של המציעים השונים לגורמים לא מוסמכים; או חישוב של השכר הממוצע מבלי לחשוף את שכרם האישי של עובדים מסוימים.
רשת תקשורת
מתמטיקאים מהמכון פיתחו שיטה לדילול רשתות, תוך שימור איכות התקשורת האפשרית בין הנקודות המרכיבות את הרשת. מדובר, לדוגמה, ברשתות תקשורת כגון רשת טלפונים, רשת מחשבים גדולה, ואפילו רשת מקומית של מחשבים מבוזרים. דרך פשוטה להקמת רשת תקשורת בין נקודות, היא הנחת קווי תקשורת ישירים בין כל נקודה לכל שאר הנקודות ברשת. אלא שברשתות שכוללות נקודות רבות מאוד, השיטה הזאת מחייבת למתוח קווים רבים מאוד, דבר שעלול להיות קשה ויקר לביצוע.
מתכנני רשתות נדרשים אפוא למצוא את שביל הזהב בין רשת צפופה, המבוססת על קווים ישירים רבים (דבר שמאפשר תקשורת מהירה במחיר גבוה), לבין רשת דלילה, שבה התקשורת בין נקודות רבות אינה ישירה, דבר שאומנם מוזיל את המחיר, אך עלול להאט את התקשורת. רשתות דלילות מסוג זה מבוססות על חלוקה לאזורים מקומיים שונים ברשת, ועל תקשורת בין-אזורית, המשרתת בעת ובעונה אחת נקודות רבות יחסית. המתמטיקאים של המכון מצאו דרך לקבוע עד כמה אפשר לדלל את הרשת, מבלי לפגוע יותר מדי ביעילות התקשורת שבין הנקודות השונות ברשת. בנוסף לכך, הציעו מדעני המכון מבנה יעיל של רשת תקשורת בין מחשבים, או בין רכיבי מחשב, המכונה "רב-פרפר", מכיוון שמראהו מזכיר כמה פרפרים השלובים זה בזה. על בסיס המחקרים האלה מתוכננות כיום רשתות תקשורת ומערכות של מחשבים מבוזרים במקומות שונים בעולם.
שפות חדשות 1
מדעני המכון פיתחו שפת מחשב - פרולוג מקבילי - המבוססת על לוגיקה, היכולה להנחות מחשבים המבצעים "עיבוד מקבילי" כלומר, מבצעים מספר פעולות בעת ובעונה אחת. מחשבים אלה מאפשרים צימצום ניכר של משך הזמן הנדרש לביצוע מטלות. בהמשך פיתחו החוקרים מערכת הפעלה חדשה - לוגיקס - שאיפשרה להשתמש בשפת הפרולוג המקבילי לפיתוח מערכות משופרות של דואר אלקטרוני וועידות מחשב מרובות-משתתפים. טכנולוגיה זו משמשת כיום לבניית "אתרי מפגש וירטואליים" ברשת האינטרנט.
שפות חדשות 2
מדען מחשב מהמכון יצר שפת מחשב חדשה ומקורית, המבוססת על שימוש במבנים חזותיים. שפה זו, הקרויה "תרשימי מיצוב", מיועדת לתיאור ברור, מדויק ואינטואיטיבי של ההתנהגות המלאה של מערכות "תגובתיות" שהן מערכות מורכבות ומסועפות, הנדרשות להגיב למצבים משתנים.
גרסה אחת של שפת תרשימי המיצוב משולבת בתפיסת הפירוק הפונקציונלי של מערכות. גרסה שנייה של השפה משולבת בתפיסה "מונחית עצמים". השפה מתאימה לתכנון, לבנייה, לניתוח ולתחזוקה של מערכות תגובתיות, על-פי דרישות התנהגות כלשהן. כלים ממוחשבים שנבנו מסביב לשפה זו מאפשרים לבחון את המערכת בהדמיה. בנוסף לכך נבנו כלים המאפשרים להמיר את השפה החזותית לשפת תכנות מקובלת, המאפשרת הדמיה על מחשב כלשהו. כך, למעשה, יכול המחשב לתכנת את עצמו - לאחר שהאיפיונים העקרוניים של המערכת הוגדרו בידי אדם - באורח אינטואיטיבי ונוח. שפת תרשימי המיצוב מקובלת כיום במקומות רבים בעולם ככלי מרכזי לתיאור מערכות בתעשיית המטוסים, בתעשיית הרכב, בתעשייה הכימית, במערכות תקשורת, ועוד.
בעקבות יצירתה של שפת "תרשימי מיצוב" נוצר תחום מחקר חדש במדעי המחשב, שבמרכזו "פורמליזמים חזותיים" למיגוון פעילויות הנדסיות וממוחשבות. תחום זה מתפתח וגדל במהירות גדולה יחסית. מדעני מחשב מכל העולם מצטרפים לתחום זה מתוך הערכה, כי האפשרויות שהוא פותח עדיין רחוקות ממיצוי.
מתמטיקה טובה לבריאות
מתמטיקה של הביולוגיה
המערכת החיסונית הפועלת בגוף כוללת גורמים רבים מאוד, בעלי אופי שונה, הממלאים תפקידים מוגדרים ומשפיעים זה על זה, וכן על סביבתם הקרובה, במערכת סבוכה עד מאוד של יחסי גומלין. במטרה להבין - ואולי אף לחזות - את אופן פעולתה של המערכת החיסונית, פיתחו המתמטיקאים של המכון, בשיתוף עם עמיתיהם האימונולוגים (מדעני תורת החיסון), דגמים מתמטיים אחדים, המתארים את פעולתם של כמה ממרכיבי המערכת החיסונית. בכמה מקרים יצרו המתמטיקאים מושגים חדשים ופיתחו תפיסות חדשות באשר לפעולתה של המערכת החיסונית. מושגים ותפיסות אלה השפיעו על דרך החשיבה שהיתה מקובלת עד אז בקרב האימונולוגים. בניסוי אחד אושר הניבוי של מודל מתמטי, על אף שלא תאם את השערתם של האימונולוגים.
כיוון מחקר זה עשוי להוביל לפיתוח כלים מתמטיים למחקר ביו-רפואי ובאימונולוגיה, וכן לסייע בפיתוח תרופות הפועלות על המערכת החיסונית, כגון תרופות נוגדות אלרגיה, או תרופות למחלות אוטו-אימוניות (מחלות שבהן המערכת החיסונית תוקפת - בטעות - את רקמות הגוף).
חישובי נשימה
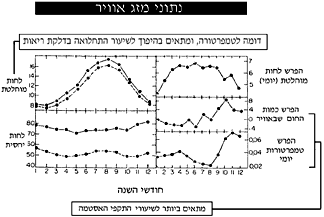
מתמטיקאים מהמכון גילו שתנודות חדות בטמפרטורה מגדילות את השכיחות והחומרה של התקפי קצרת (אסטמה). המחקר התבסס על נתונים שנאספו ב- 8,650 בדיקות של חולים בדרכי הנשימה. החוקרים מצאו קשר בין נתוני שכיחות ההתקפים, לבין ההופעה של תנאים מטאורולוגיים מסוימים.
החוקרים השמיטו מן התמונה מגמות אנומליות כמו, למשל, המספר הרב של בעיות נשימה שנרשמו בחדר-המיון בשבתות, כתוצאה ישירה מחוסר האפשרות לפנות למרפאות קופת-חולים. ממצאי המחקר מסבירים את שני השיאים בכמותם של התקפי הקצרת: בראשית הסתיו ובראשית האביב. לעומת זאת, לא נמצא מיתאם מובהק בין דפוסי השכיחות של דלקת-ריאות לבין דפוסי השכיחות של התקפי קצרת.
מחקרים אלה עשויים לסייע בגיבוש נוסחה שתקבע את תנאי האקלים הנוחים לילדים רגישים, וכן בקביעת הזמנים המתאימים לשימוש בתרופות, דבר שעשוי להפחית במידה ניכרת את צריכתן.