קווזי-גבישים הם חומרים בעלי תכונות הולכה טופולוגיות. כך עולה ממחקר עצמאי שביצעו חמישה תלמידי מחקר במכון.
הסיפור מתחיל בשתי נקודות נפרדות בבניין הפיסיקה. בנקודה אחת, במעבדתו של
פרופ' ירון זילברברג, עסקו תלמידי המחקר יואב לחיני ומור ורבין בניסויים במערכות אופטיות של קווזי-גבישים. הקווזי-גבישים, שהתגלו לפני כ-30 שנה, מתאפיינים בסידור ייחודי של אטומים: בדומה לגבישים רגילים, הם בעלי ארגון פנימי, אך בניגוד אליהם, ארגון זה אינו מחזורי. ההכרה בעובדה שקווזי-גבישים הם סוג חדש של חומר מוצק חוללה מהפכה במדעי החומרים, הובילה לעדכון ההגדרה הרשמית לגבי מהותו של גביש, ועוררה עניין רב בקרב חוקרי גבישים, כימאים, פיסיקאים ומתמטיקאים כאחד. מגלה התופעה, פרופ' דן שכטמן מהטכניון, זכה בעקבות תגלית זו בפרס נובל בכימיה. יואב ומור, אשר בחנו תכונות הולכה בסוג חדש של קווזי-גבישים אופטיים אשר פותחו במכון, הבחינו בתופעות מוזרות המתחוללות בקצותיהם, על פני השטח שלהם, ומדדו אותן, אך לא ידעו להציע להן הסבר.
בצידו השני של בניין הפיסיקה נחשפו תלמידי המחקר עודד זילברברג, מקבוצתו של פרופ' יובל גפן, קובי קראוס מקבוצתו של פרופ' עדי שטרן, וזוהר רינגל מקבוצתו של פרופ' אהוד אלטמן, לתחום מחקר אחר, צעיר ומסקרן – חומרים טופולוגיים. חומרים אלו, שהתגלו בשנת 2007, הם גבישים מחזוריים "רגילים", אך בעלי תכונות חשמליות מוזרות: בעוד שחלקו הפנימי של החומר מתפקד כמבודד, פני השטח שלו מוליכים חשמל כאילו היו עשויים ממתכת. גילוי החומרים האלה שינה את התפיסה המקובלת באשר לתכונות חשמליות של חומרים, אשר הפרידה בין חומרים שבהם יש תנועה חופשית של אלקטרונים, לבין אלה שאינם מאפשרים תנועה כזו. מדענים העוסקים בפיסיקה של חומר מעובה מנסים מאז לגלות חומרים טופולוגיים נוספים, ולחקור את תכונותיהם.
שלושת הסטודנטים שאלו את עצמם, האם קווזי-גבישים עשויים להיות בעלי תכונות טופולוגיות. מחקרים מסוימים, המתייחסים לחומרים טופולוגיים כאל הטלות של מערכות מממדים רבים יותר, רמזו שהתשובה לשאלה זו עשויה להיות חיובית: גם את הקווזי-גבישים אפשר להציג באופן מתמטי כהטלות של מערכת מחזורית ממימד גבוה יותר. למרות המאמצים שהשקיעו, לא הצליחו השלושה לזהות תופעות טופולוגיות במודלים של מערכות קווזי-גבישים.
הקו שחיבר בסופו של דבר בין שתי הנקודות לא היה ישר כלל – הוא עבר הרחק מבניין הפיסיקה, דרך שדרות ח"ן בתל אביב. שם, ביום שבת אחד אחר-הצהריים, נפגשו במקרה יואב ועודד. עם ההבנה שייתכן כי ממצאיהם משלימים זה את זה, קבעו לקיים מפגש בין התיאורטיקנים לניסיונאים.
בעקבות המפגש הזה הבינו חמשת תלמידי המחקר, כי יש בידיהם קצה החוט שביקשו. בהמשך, הם הצליחו להוכיח באופן תיאורטי ובאמצעות מדידות ניסיוניות, שקווזי-גבישים הם אכן חומרים בעלי תכונות טופולוגיות. יתר על כן, בעוד שמבחינות מסוימות התכונות הטופולוגיות של הקווזי-גבישים דומות לתכונות של חומרים טופולוגיים "רגילים", מבחינות אחרות הן שונות מאוד.
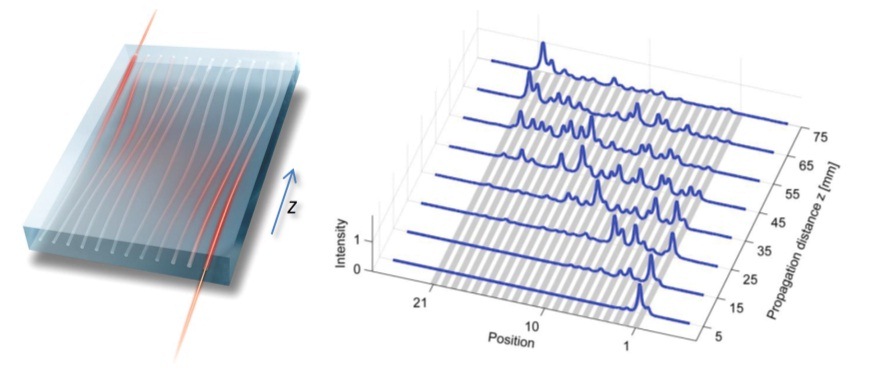
בניסויים שבוצעו במעבדתו של פרופ' ירון זילברברג יצרו חברי הצוות קווזי-גביש חד-ממדי, ומדדו את תכונות ההולכה האופטית על שפתו. קווזי-גביש זה בנוי מקוביית זכוכית שבתוכה נצרב בלייזר מערך של סיבים אופטיים מקבילים, במירווחים קווזי-מחזוריים. הניסויים הראו, שכאשר אור מוחדר לסיב מרכזי במערך, הוא "מדלג" בין סיבים סמוכים, ויוצא – מצדו השני של המערך – מכל הסיבים בעת ובעונה אחת. לעומת זאת, כאשר האור מוחדר לסיב קיצוני, הוא אינו מדלג כלל, ויוצא מהסיב אליו הוכנס. ניסוי זה הוכיח את קיומם של מצבי שפה במערכת – כלומר, תכונות ייחודיות לפני השטח שלה. התופעה מקבילה לזרם חשמלי בחומר טופולוגי, שנע רק על השטח, מבלי לחדור לתוך החומר. ממצא ראשוני זה היה מפתיע, שכן הדעה הרווחת בקרב אנשי החומרים הטופולוגיים הייתה, שהתנהגות כזו אינה קיימת במערכות חד–ממדיות.
בניסוי נוסף השתמשו במערכת דומה, שבה המרחק בין הסיבים האופטיים משתנה לאורך המערך. בסידור נכון של הסיבים מדלג אור שהוחדר לסיב קיצוני בצדה האחד של המערכת דרך המערכת כולה, ויוצא דרך הסיב הקיצוני שמצדה השני של המערכת. תופעה מפתיעה זו, הקרויה "משאבה טופולוגית", מוכיחה כי התופעות שנראו בניסויים הן אכן בעלות טבע טופולוגי.
התיאוריה שפיתחו חברי הצוות מציעה הסבר לשאלה, מדוע קווזי-גבישים חד-ממדיים מתנהגים בדרך זו. את המודל שאיתו עבדו אפשר לתאר כסוג של חיתוך חד-ממדי של מערכת תופעת הול הקוונטית, הדו-ממדית. באופן מפתיע, החיתוך שומר על התכונות הטופולוגיות של המערכת הדו-ממדית, וכך "יורשים"הקווזי-גבישים החד-ממדיים את התכונות הטופולוגיות שלהם מה"אבות הקדומים" שלהם – הגבישים המחזוריים.
ממצאים אלה
פורסמו באחרונה בכתב-העת המדעי
Physical Review Letters, והמאמר נבחר כ"בחירת העורך" בכתב-העת
Science ובכתבי-עת נוספים. במחקרי ההמשך בודקים חברי הצוות, בין היתר, האם אפשר להכליל את התוצאות האלה לממדים נוספים. לדוגמה, התיאוריה שפיתחו חברי הצוות מרמזת שקווזי-גבישים תלת-ממדיים יכולים להציג תופעות הולכה על פני השטח, שתכונותיהם נובעות ממערכות טופולוגיות שש-ממדיות.